Завдання № 9.18

№ 9.18 Геометрія =  № 17.18 Математика

Діагональ прямокутника дорівнює 10 см. Знайдіть периметр чотирикутника, вершинами якого є середини сторін цього прямокутника.

Розв'язок:

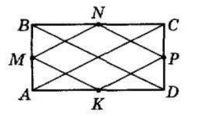
AC і BD — діагоналі прямокутника ABCD; точки M, N, P, і K — середини його сторін. MN — середня лінія ΔABC,  
MN = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 10 см = 5 см.  
KP — середня лінія ΔACD,  
KP = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 10 см = 5 см.  
MN || AC, KP || AC, тому MN || KP за ознакою паралельних прямих.  
NP — середня лінія ΔBCD,  
NP = $\frac{1}{2}$ BD = $\frac{1}{2}$ · 10 см = 5 см (діагоналі прямокутника рівні).  
MK — середня лінія ΔABD,  
MK = $\frac{1}{2}$ BD = $\frac{1}{2}$ · 10 см = 5 см.  
NP || BD, MK || BD, тоді NP || MK.  
Отже, MNPК — паралелограм за означенням.  
NP = MK = KP = MN = 5 см, тому MNPК — ромб.  
P_MNPK = 4 · 5 = 20 см. 

Відповідь:

20 см.