Завдання № 9.17

№ 9.17 Геометрія =  № 17.17 Математика

E, F, G, H − середини сторін AB, BC, CD і DA опуклого чотирикутника ABCD. Знайдіть периметр чотирикутника EFGH, якщо AC = 16 см, BD = 10 см.

Розв'язок:

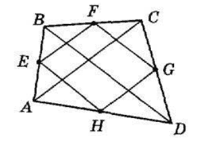
E, F, G, H − середини сторін AB, BC, CD і DA опуклого чотирикутника ABCD. Знайдіть периметр чотирикутника EFGH, якщо AC = 16 см,
BD = 10 см.
Проведемо діагоналі AC і BD чотирикутника EFGH.  
У ΔABC EF — середня лінія,
EF || AC, EF = $\frac{1}{2}$ AC.  
У ΔACD HG — середня лінія, HG || AC, HG = $\frac{1}{2}$ AC.  
Отже, EF = HG = $\frac{1}{2}$ AC =
= $\frac{1}{2}$ · 16 см = 8 см.  
Аналогічно FG — середня лінія ΔBCD, 
EH — середня лінія ΔABD, FG || BD,
FG = $\frac{1}{2}$ BD;
EH || BD, EH = $\frac{1}{2}$ BD.
FG = EH = $\frac{1}{2}$ · 10 см = 5 см.  
P_EFGH = 2 · (8 + 5) = 26 (см).  

Відповідь:

26 см.