№ 9.16 Геометрія = № 17.16 Математика
Одна зі сторін трикутника дорівнює 10 см, а одна із середніх ліній − 6 см. Знайдіть дві інші сторони трикутника, якщо одна з них у 1,5 раза більша за другу. Скільки випадків слід розглянути?
Розв'язок:
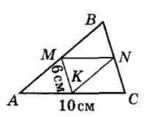
Нехай в ΔABC AC = 10 см, M — середина AB, N — середина BC, K — середина AC.
MN не може дорівнювати 6 см,
бо MN = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 10 = 5 (см).
Нехай MK = 6 см. Можливі два випадки:
1. Сторона AB у 1,5 рази більша за BC.
BC = 2MK = 2 · 6 = 12 (см).
AB = 1,5 · BC = 18 (см).
2. Сторона BC у 1,5 рази більша за AB.
BC = 2MK = 2 · 6 = 12 (см).
AB = BC : 1,5 = 12 : 1,5 = 8 (см).
Відповідь:
1. 12 см і 18 см;
2. 12 см, 8 см.
