№ 9.14 Геометрія = № 17.14 Математика
Сторони трикутника відносяться як 4 : 3 : 5. Знайдіть його сторони, якщо периметр трикутника, утвореного середніми лініями даного трикутника, дорівнює 60 см.
Розв'язок:
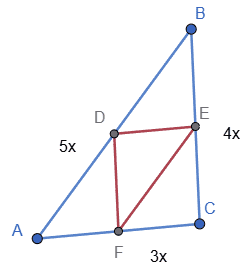
Нехай x — коефіцієнт пропорційності. Тоді сторони трикутника дорівнюють 4x, 3x і 5x. Відповідні їм середні лінії вдвічі менші:
$\frac{4x}{2}\ ;\ \frac{3x}{2};\ \frac{5x}{2}.\ $
Периметр трикутника, утвореного середніми лініями, дорівнює:
$\frac{4x}{2}\ +\ \frac{3x}{2}\ +\ \frac{5x}{2}\ =\ \frac{12x}{2}\ =\ 6x. $
Отже, 6x = 60, звідки x = 10.
Сторони трикутника:
4 · 10 = 40 (см);
3 · 10 = 30 (см);
5 · 10 = 50 (см).
Відповідь:
40 см, 30 см, 50 см.
