Завдання № 8.9

№ 8.9 Геометрія =  № 16.9 Математика

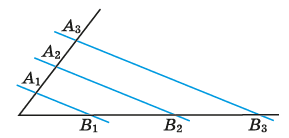
На малюнку A₁A₂ = A₂A₃, A₁B₁ || A₂B₂ || A₃B₃. 
A₁A₂ : B₁B₂ = 3 : 5, B₂B₃ – A₂A₃ = 8 см. Знайдіть A₁A₂, A₂A₃, B₁B₂, B₂B₃. 

Розв'язок:

За умовою A₁A₂ : B₁B₂ = 3 : 5.  
Оскільки за теоремою Фалеса $\frac{A_1A_2}{A_2A_3}$ = $\frac{B_1B_2}{B_2B_3}$, то $\frac{A_2A_3}{B_2B_3}$ = $\frac{3}{5}.$
За умовою B₂B₃ – A₂A₃ = 8 см. 
Нехай A₂A₃ = x см, тоді B₂B₃ = (x + 8) см.  
$\frac{A_1A_2}{B_1B_2}$ = $\frac{A_2A_3}{B_2B_3}$;
$\frac{3}{5} = \frac{x}{x\ +\ 8}; $
5x = 3x + 24; 
2x = 24; 
x = 12.  
Отже, A₁A₂ = A₂A₃ = 12 (см); 
B₁B₂ = B₂B₃ = 12 + 8 = 20 (см).  

Відповідь:

12 см, 20 см.