№ 8.14 Геометрія = № 16.14 Математика
Точка K — середина медіани AD трикутника ABC. Відрізок BK перетинає сторону AC у точці M. Знайдіть AM : MC.
Розв'язок:
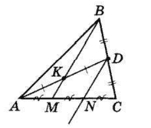
За умовою D — середина BC, K — середина AD.
Проведемо DN || BK. Паралельні прямі BM і DN перетинають сторону трикутника DAC. AK = KD, значить, AM = MN.
Паралельні прямі BM і DN перетинають сторону кута BCA.
За умовою BD = DC, значить, MN = NC.
Отже, AM = MN = NC. Тоді AM : MC = 1 : 2.
