Завдання № 8.13

№ 8.13 Геометрія =  № 16.13 Математика

Точки M і N ділять медіану AD трикутника ABC на три рівні частини (AM = MN = ND). Доведіть, що пряма BN містить медіану трикутника. 

Розв'язок:

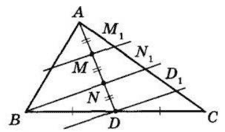
Проведемо через точки M і D прямі, паралельні прямій BN. Оскільки AM = MN = ND за умовою, то AM₁ = M₁N₁ = N₁D₁ за теоремою Фалеса відносно кута DAC. 
Сторони кута ACB перетинають паралельні прямі DD₁ і NN₁. Оскільки CD = DB за умовою, то за теоремою Фалеса CD₁ = N₁D₁.  
Отже, AM₁ = M₁N₁ = N₁D₁ = D₁C, звідки AN₁ = N₁C, тобто N₁ — середина AC, BN₁ містить медіану трикутника.