Завдання № 8.12

№ 8.12 Геометрія =  № 16.12 Математика

Точки E, F і G ділять медіану AD трикутника ABC на чотири рівні частини (AE = EF = FG = GD). Доведіть, що пряма СG ділить сторону AB у відношенні 3 : 2, починаючи від вершини A.

Розв'язок:

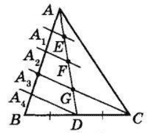
Проведемо через точки E, F і D прямі, паралельні прямій CG. Вони поділять сторону AB на 5 рівних відрізків AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄B.  
AA₁ = A₁A₂ = A₂A₃ = за теоремою Фалеса, застосованою до кута BAD.  Розглянемо ∠CBA. За умовою D — середина BC; DA₄ || GA₃ за побудовою, значить, за теоремою Фалеса BA₄ = A₃A₄.  
Отже, всі п’ять відрізків рівні. Відрізок AA₃ містить три таких відрізки, A₃B — два. Отже, AA₃ : A₃B = 3 : 2.