№ 7.12 Геометрія = № 15.12 Математика
Трапеція вписана в коло радіуса R так, що діаметр кола є її більшою основою. Знайдіть периметр трапеції, якщо її менша основа дорівнює бічній стороні.
Розв'язок:
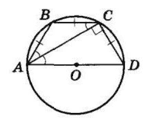
Трапеція ABCD вписана в коло, значить, вона рівнобічна (за наслідком із властивості вписаного чотирикутника).
AB = BC = CD за умовою.
Проведемо діагональ AC.
∠BCA = ∠CAD як внутрішні різносторонні при BC || AD і січній AC.
В ΔABC ∠BAC = ∠BCA як кути при основі рівнобедреного ΔABC. ∠ACD = 90°, бо спирається на діаметр AD.
Нехай ∠BAC = ∠CAD = ∠BCA = x.
Сума протилежних кутів вписаного чотирикутника дорівнює 180°:
x + x + x + 90 = 180;
3x = 90;
x = 30.
Отже, ∠CAD = 30°.
Тоді в ΔACD (∠C = 90°) CD =
= $\frac{1}{2}$ AD = $\frac{1}{2}$ · 2R = R як катет, що лежить проти кута 30°.
PABCD = R + R + R + 2R = 5R.
Відповідь:
5R.
