№ 7.11 Геометрія = № 15.11 Математика
Точка M лежить на стороні AB гострокутного трикутника ABC. MP і MK — перпендикуляри до сторін AC і BC відповідно. Доведіть, що навколо чотирикутника MPCK можна описати коло, діаметром якого буде відрізок CM.
Розв'язок:
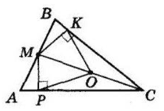
В ∆ABC M ∈ AB, MP ⊥ AC, MK ⊥ BC. Проведемо MC і позначимо точку O — середину MC. В ∆МКС середина гіпотенузи O — центр описаного кола, OM = OK = OC — радіус цього кола.
Аналогічно в ∆MPC OP = OM = OK — радіуси описаного кола з центром O. Таким чином точки P, M, K і C рівновіддалені від точки O. Тоді O — центр кола, описаного навколо прямокутника MPCK, MC — діаметр цього кола.
