Завдання № 7.10

№ 7.10 Геометрія =  № 15.10 Математика

У гострокутному трикутнику ABC проведено висоти AH₁, BH₂, які перетинаються в точці H. Доведіть, що навколо чотирикутника CH₁HH₂ можна описати коло, діаметром якого буде відрізок CH.

Розв'язок:

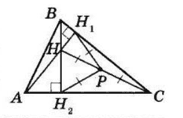
У ∆ABC AH₁ ⊥ BC, BH₂ ⊥ AC, H — точка перетину AH₁ і BH₂. Проведемо HC і позначимо точку P — середину HC. Середина P гіпотенузи HC — центр описаного навколо прямокутного ∆HH₁C кола, а PH = PH₁ = PC — його радіуси. 
Аналогічно, точка P — центр кола, описаного навколо прямокутника ∆H₂HC, і PH = PH₂ = PC – радіуси цього кола. Таким чином, точки H, H₁, C і H₂ рівновіддалені від точки P, тобто лежать на колі з центром P і діаметром HC, описаному навколо чотирикутника HH₁CH₂.