№ 6.33 Геометрія = № 14.33 Математика
Менша основа рівнобічної трапеції дорівнює бічній стороні, а діагональ перпендикулярна до бічної сторони. Знайдіть кути трапеції.
Розв'язок:
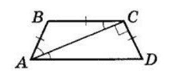
У трапеції ABCD AB = BC = CD, AC ⊥ CD.
У ΔABC ∠BAC = ∠BCA як кути при основі рівнобедреного трикутника.
∠BCA = ∠CAD як внутрішні різносторонні при AD || BC і січній AC.
Тоді ∠BAC = ∠CAD,
∠CDA = ∠BAD = 2∠CAD.
Нехай ∠CAD = x, тоді ∠CDA = 2x.
З ΔACD x + 2x = 90;
3x = 90;
x = 30.
Тоді ∠BAD = ∠CDA = 2 · 30° = 60°.
∠ABC = ∠BCD = 180 – 60 = 120
Відповідь:
60°, 120°.
