№ 6.27 Геометрія = № 14.27 Математика
У рівнобічній трапеції діагональ утворює з меншою основою кут 40°. Знайдіть кути трапеції.
Розв'язок:
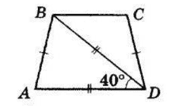
ΔABD — рівнобедрений (AD = BD за умовою).
∠DAB = ∠DBA = (180° − ∠BDA) : 2 =
= (180° − 40°) : 2 = 140° : 2 = 70°.
∠CDA = ∠DAB = 70° (як кути при основі).
∠BDC = ∠CDA − ∠BDA = 70° − 40° = 30°.
∠CBD = ∠BDA = 40° (як внутрішні різносторонні при BC || AD і січній BD).
В ΔBCD ∠C = ∠ABC = ∠ABD + ∠CBD =
= 70° + 40° = 110°.
Відповідь:
70°, 110°, 110°, 70°.
