№ 6.25 Геометрія = № 14.25 Математика
У прямокутній трапеції гострий кут дорівнює 60°. Більша бічна сторона й більша основа дорівнюють по 16 см. Знайдіть меншу основу.
Розв'язок:
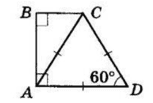
ABCD — трапеція, ∠A = ∠B = 90°,
∠D = 60°,
AD = CD = 16 см. Проведемо діагональ AC.
ΔACD — рівнобедрений, ∠D = 60°, тоді
∠CAD = ∠DCA = 60°, ΔACD — рівносторонній,
AC = AD = CD = 16 см.
В ΔABC ∠BAC = ∠A − ∠CAD =
= 90° − 60° = 30°.
BC = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 16 см = 8 см як катет проти кута 30°.
Відповідь:
8 см.
