№ 6.20 Геометрія = № 14.20 Математика
У трапеції ABCD BC — менша основа. На відрізку AD взято точку E так, що BE || CD;
∠ ABE = 60°, ∠ BEA = 40°. Знайдіть кути трапеції.
Розв'язок:
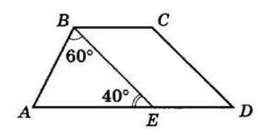
В ∆АВЕ ∠А = 180° − (∠АВЕ + ∠ВЕА) =
= 180° − (60° + 40°) = 80°.
∠АВС = 180° − ∠А = 180° − 80° = 100°.
∠CDA = ∠BEA = 40° як відповідні
при BE || CD і січній AD.
∠BCD = 180° − ∠D = 180° − 40° = 140°.
Відповідь:
80°, 100°, 140°, 40°.
