№ 5.26 Геометрія = № 9.26 Математика
На сторонах квадрата зовні побудовано рівносторонні трикутники. Доведіть, що вершини трикутників, які не є вершинами заданого квадрата, є вершинами іншого квадрата.
Розв'язок:
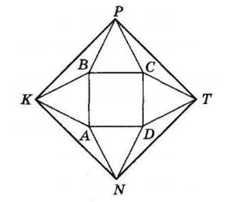
Розглянемо трикутники ABK, BCP, CDT, DAN.
Оскільки вони рівносторонні і побудовані на сторонах квадрата,
то BK = BP = CP = CT = DT = DN = AN = AK і всі кути цих трикутників дорівнюють 60°.
У квадрата ABCD ∠A = ∠B = ∠C = ∠D = 90°.
Тоді ∠KBP = ∠PCT = ∠TDN = ∠NAK =
= 360° − (90° + 60° + 60°) = 150°.
∆AKP = ∆PCT = ∆TDN = ∆NAK за двома сторонами і кутом між ними.
Тоді KP = PT = TN = NK і KPTN — ромб.
∠KPT = ∠KPB + ∠BPC + ∠TCP, де ∠BPC = 60°,
∠KPB = ∠TPC (із рівності трикутників) і
KPB =TPC = $\frac{180° - 150°}{2} = 15°$
Тоді ∠KPT = 15° + 60° + 15° = 90°.
Ромб, у якого один з кутів прямий, є квадратом.
Отже, KPTN — квадрат.
