№ 5.25 Геометрія = № 9.25 Математика
У рівнобедрений прямокутний трикутник ABC (∠ C = 90^° ) вписано квадрат KMNL так, що точки K і M лежать на гіпотенузі трикутника, а точки L і N — на катетах AC і BC відповідно. Периметр квадрата дорівнює 12 см. Знайдіть гіпотенузу трикутника.
Розв'язок:
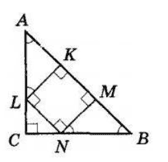
∆ABC — прямокутний і рівнобедрений, тому ∠A = ∠B = 45°.
LK ⊥ AB за умовою, тоді в ∆ALK,
∠ALK = 45° і ∆ALK — рівнобедрений, тому LK = AK.
Аналогічно в ∆NMB, NM = MB.
PLNMK = 12 см, тоді MK = 12 : 4 = 3 см.
AB = AK + KM + MB = 3MK = 3 · 3 = 9 см.
Відповідь:
9 см.
