Завдання № 5.24

№ 5.24 Геометрія =  № 9.24 Математика

У рівнобедреній прямокутній трикутник ABC (∠ C = 90°) вписано квадрат CMNK  так, що прямий кут у ньому спільний, а точка N належить стороні AB. Катет трикутника дорівнює b см. Знайдіть периметр квадрата.

Розв'язок:

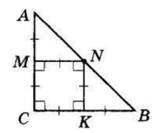
У ∆ABC кут C = 90°, CA = CB = b см, CMNK — квадрат, вписаний у ∆ABC.  ∆ABC — прямокутний і рівнобедрений.  
Тоді ∠CAB = ∠CBA = 45°.    
У ∆NKB ∠NKB = 90° як суміжний із прямим кутом, ∠NBK = 45°, 
тоді ∠BNK = 90° − 45° = 45°.  
∆NKB — прямокутний і рівнобедрений, NK = BK.   
MN = CK, як протилежні сторони квадрата.  
Отже, катет дорівнює двом сторонам квадрата.  
P_CMNK = 2CB = 2b (см).  

Відповідь:

2b см.