№ 5.23 Геометрія = № 9.23 Математика
До кола із центром у точці O з точок A проведено дві взаємно перпендикулярні дотичні AB і AC , B і C — точки дотику. Доведіть, що ABOC — квадрат.
Розв'язок:
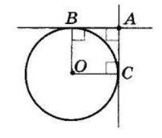
AC ⊥ AB за умовою, OB ⊥ AB, як радіус, проведений у точку дотику, тоді AC || OB.
Аналогічно OC ⊥ AB.
Тоді ABOC — паралелограм за означенням.
OB = OC, як радіуси кола.
Тому ABOC — ромб.
Кут A = 90° за умовою, отже, ABOC — квадрат.
