№ 5.22 Геометрія = № 9.22 Математика
ABCD — квадрат, AE = AF = CG = CH. Доведіть, що EFGH — прямокутник.
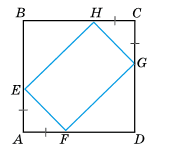
Розв'язок:
∆AEF = ∆CHG за двома катетами (AE = AF = CG = CH за умовою).
Тоді EF = HG. Оскільки сторони квадрата рівні, то EB = BH = GD = DF.
Тому ∆EBM = ∆GDF за двома катетами, звідки EH = FG.
EFGH — паралелограм (протилежні сторони попарно рівні).
∆EBH, ∆HCG, ∆EAF, ∆GDF є рівнобедреними прямокутними, їх гострі кути дорівнюють 45°.
∠EGH = 180° − (∠BHE + ∠CHG) =
= 180° − (45° + 45°) = 90°.
Отже, EFGH — прямокутник за ознакою.
