№ 5.21 Геометрія = № 9.21 Математика
ABCD — квадрат, AE = FC. Доведіть, що BEDF — ромб.
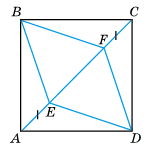
Розв'язок:
∆ABE = ∆CBF = ∆CDF = ∆ADE рівні за двома сторонами і кутом між ними
(AB = BC = CD = AD, AE = CF за умовою,
∠BAE = ∠BCF = ∠DCF = ∠DAE за властивістю діагоналей).
Тоді BE = BF = DE = DF, EBFD — паралелограм і ромб (протилежні сторони попарно рівні).
