Завдання № 5.20

№ 5.20 Геометрія =  № 9.20 Математика

Периметр квадрата дорівнює 32 см. Знайдіть відстань від точки перетину діагоналей квадрата до його сторін. 

Розв'язок:

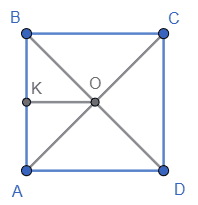
ABCD — квадрат, O — точка перетину його діагоналей; OK ⊥ AB — відстань від точки O до сторони квадрата.  

P_ABCD = 32 см, тоді AB = 32 : 4 = 8 см.

В ∆ABO OA = OB, OA ⊥ OB за властивістю діагоналей.

OK – висота і медіана, AK = KB = $\frac{1}{2}$ · AB = $\frac{1}{2}$ · 8 = 4 см.

∆OBK — рівнобедрений, AK = OK = 4 см.  

Відповідь:

4 см.