№ 4.34 Геометрія = № 8.34 Математика
Доведіть, що середини сторін прямокутника є вершинами ромба.
Розв'язок:
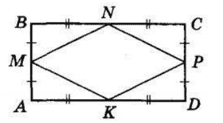
ABCD — прямокутник. Точки M, N, P, K — середини його сторін.
△MBN = △PCN = △PDK = △MAK за двома катетами (протилежні сторони прямокутника рівні, а значить, рівні і їх половини). З рівності трикутників випливає, що MN = NP = PK = MK.
Тоді MNPK — паралелограм (протилежні сторони попарно рівні), а оскільки всі сторони рівні, то MNPK — ромб.
