№ 4.33 Геометрія = № 8.33 Математика
На діагоналі AC ромба ABCD позначено точки M і N так, що AM = CN. Доведіть, що чотирикутник DMBN є ромбом (розгляньте два випадки розміщення точок M і N).
Розв'язок:
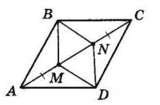
1 випадок
ABCD — ромб, тому AB = BC = CD = AD.
AM = CN за умовою.
∠BAM = ∠DAM = ∠BCN = ∠DCN за властивістю ромба.
Тоді △AMB = △AMD = △CNB = △CND за двома сторонами і кутом між ними.
Звідси BM = BN = DN = DM.
∠BNC = ∠DNC = ∠BMA = ∠DMA, тоді ∠BNM = ∠DNM = ∠BMN = ∠DMN як суміжні з рівними кутами, а вони є внутрішніми різносторонніми при прямих BN і MD та BM і ND та січній MN.
Тоді BN || MD, BM || ND.
MBND — паралелограм, у якого всі сторони рівні, тобто, ромб.
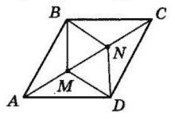
2 випадок
ABCD — ромб, AC — його діагональ, AM = CN.
△ABM = △CDN за двома сторонами і кутом між ними (AB = CD, AM = CN за умовою, ∠BAM = ∠DCN за властивістю діагоналей). З рівності трикутників BM = DN, ∠BMA = ∠DNC. Ці кути внутрішні різносторонні при прямих BM і DN і січній NM.
Тоді BM || DN. У чотирикутнику BMDN протилежні сторони BM і DN паралельні й рівні.
Отже, BMDN — паралелограм. Аналогічно, △ABM = △CBN за двома сторонами і кутом між ними.
Тому BM = BN. Паралелограм BMDN, у якого сусідні сторони BM і BN рівні — це ромб.
