№ 4.31 Геометрія = № 8.31 Математика
Діагональ ромба, проведена з вершини тупого кута, утворює з висотою, проведеною із цієї самої вершини, кут 30°. Менша діагональ ромба дорівнює a см. Знайдіть:
1. кути ромба;
2. периметр ромба.
Розв'язок:
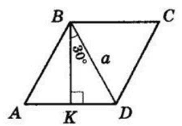
ABCD — ромб, BD — менша діагональ, BD = a см,
BK ⊥ AD, ∠KBD = 30°.
1. З △BКD ∠BDK = 90° − ∠KBD = 90° − 30° = 60°.
Тоді ∠D = 2 · ∠KBD = 2 · 60° = 120° (за властивістю діагоналі ромба).
∠B = ∠D = 120°, ∠A = ∠C =
= 180° − ∠D = 180° − 120° = 60°.
2. Рівнобедрений трикутник з кутом 60° при вершині є рівностороннім.
AB = AD = BD = a см, PABCD = 4a см.
Відповідь:
4a см.
