№ 3.9 Геометрія = № 7.9 Математика
Доведіть, що коли в чотирикутнику три кути прямі, то цей чотирикутник — прямокутник.
Розв'язок:
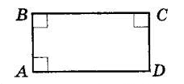
Нехай в чотирикутнику ABCD ∠A = ∠B = ∠C = 90°.
∠A і ∠B — внутрішні односторонні при прямих AD і BC і січній AB.
Оскільки їх сума дорівнює 90° + 90° = 180°, то AD || BC.
Аналогічно, сума внутрішніх односторонніх кутів B і C дорівнює 180°, тому AB || CD. ABCD — паралелограм, як чотирикутник, у якого протилежні сторони попарно паралельні.
Оскільки у паралелограма ABCD є прямий кут, то ABCD — прямокутник.
