№ 3.28 Геометрія = № 7.28 Математика
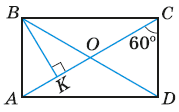
На малюнку ABCD — прямокутник, BK ⊥ AC, ∠ ACD = 60°, AB = b. Знайдіть BD і OK.
Розв'язок:
∠BAC = ∠ACD = 60° як внутрішні різносторонні при AB || CD і січній BD.
ΔAOB — рівнобедрений (AO = BO за властивістю діагоналей прямокутника) з кутом 60° при основі.
Тоді ΔAOB — рівносторонній.
AB = BO = AO = b.
BD = 2BO = 2b за властивістю діагоналей прямокутника.
В ΔAOB BK — висота і медіана.
OK = $\frac{1}{2} AO = \frac{1}{2} b = \frac{b}{2}.$
Відповідь:
2b; $\frac{b}{2}.$
