№ 3.27 Геометрія = № 7.27 Математика
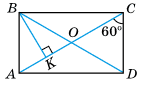
На малюнку ABCD — прямокутник, BK ⊥ AC, ∠ ACD = 60°:
1. OK = a. Знайдіть: DB і AB;
2. AC = m. Знайдіть: AK і CD.
Розв'язок:
1. ∠BAC = ∠ACD = 60° як внутрішні різносторонні при AB || CD і січній BD.
ΔABO — рівнобедрений, AO = OB за властивістю діагоналей прямокутника.
Тоді ∠ABO = ∠OAB = 60° як кути при основі.
∠AOB = 180° − 2 · 60° = 60°.
ΔAOB — рівносторонній. Висота BK є медіаною.
AO = 2AK = 2a.
AB = AO = 2a;
BD = 2BO = 2 · 2a = 4a.
2. В ΔACD (∠D = 90°) ∠CAD = 90° − 60° = 30°.
Тоді CD = $\frac{1}{2} AC = \frac{1}{2}m$ як катет, протилежний куту 30°.
∠BAC = ∠ACD = 60° як внутрішні різносторонні при AB || CD і січній BD.
ΔABO — рівнобедрений (AO = BO за властивістю діагоналей прямокутника) з кутом 60° при основі.
Тоді ΔAOB — рівносторонній.
AB = BO = AO = $\frac{m}{2}. $
BK — висота і медіана.
AK = $\frac{1}{2} AO = \frac{1}{2} · \frac{m}{2} = \frac{m}{4}. $
Відповідь:
1. 4a і 2a;
2. $\frac{m}{4}; \frac{m}{2}.$
