№ 3.23 Геометрія = № 7.23 Математика
Точки B і D належать колу із центром O, AC — діаметр кола, AD = BC. Доведіть, що ABCD — прямокутник.
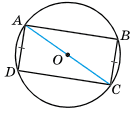
Розв'язок:
AC — діаметр кола, тому ΔABC і ΔADC — прямокутні.
ΔABC = ΔCDA за катетом і гіпотенузою (AD = BC за умовою, AC — спільна гіпотенуза).
Звідси ∠CAD = ∠ACB.
Ці кути внутрішні різносторонні при прямих AD і BC і січній AC, тому AD || BC.
ABCD — паралелограм за ознакою (AD || BC, AD = BC).
ABCD — прямокутник за ознакою, як паралелограм, який має прямий кут.
