№ 3.22 Геометрія = № 7.22 Математика
У паралелограмі ABCD з гострим кутом A діагоналі перетинаються в точці O. На відрізках AO і OC позначено точки M і N так, що OM = OB, ON = OD. Доведіть, що BMDN — прямокутник.
Розв'язок:
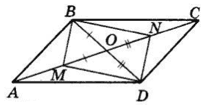
ABCD — паралелограм,
O — точка перетину його діагоналей.
OM = OB, ON = OD.
ΔBON = ΔMOD за двома сторонами і кутом між ними (BO = MO, DO = NO за умовою, ∠BON = ∠MOD як вертикальні).
BO = OD за властивістю діагоналей паралелограма.
Тоді MO = BO = ON = OD і BDО = MN.
Трикутники MOD і BON — рівнобедрені, їх кути при основі рівні.
З рівності трикутників випливає, що BN = MD, ∠BNO = ∠DMO, а ці кути є внутрішніми різносторонніми при прямих BN і MD і січній MN.
Отже, BN || MD.
MBND — паралелограм (BN || MD, BN = MD).
Раніше довели, що BD = MN, тому MBND — прямокутник.
