№ 3.21 Геометрія = № 7.21 Математика
У прямокутнику ABCD діагоналі перетинаються в точці O. OP — бісектриса трикутника AOB, ∠ DOP = 130°. Знайдіть ∠ CAB.
Розв'язок:
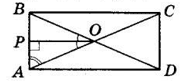
ABCD — прямокутник,
O — точка перетину його діагоналей;
OP — бісектриса ΔAOB; ∠DOP = 130°.
ΔAOB — рівнобедрений, AO = BO як половини рівних діагоналей.
Тоді бісектриса OP є медіаною і висотою.
∠BOP = 180° − ∠DOP = 180° − 130° = 50° (як суміжні).
∠AOP = ∠BOP = 50° за умовою.
З ΔAOP (∠P = 90°) ∠OAP = 90° − 50° = 40°.
Отже, ∠CAB = 40°.
Відповідь:
40°.
