№ 3.20 Геометрія = № 7.20 Математика
У прямокутнику ABCD діагоналі перетинаються в точці O, E — середина AB, ∠ CAB = 70°. Знайдіть ∠ DOE.
Розв'язок:
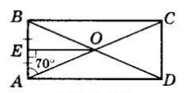
ABCD — прямокутник,
O — точка перетину його діагоналей;
BE = AE; ∠CAB = 70°.
У ΔAOB AO = BO як половини рівних діагоналей.
За умовою OE — медіана рівнобедреного ΔAOB.
Значить, OE ⊥ AB.
У ΔAOE ∠AOE = 90° − ∠OAE = 90° − 70° = 20°.
OE — бісектриса ∠AOB:
∠BOE = ∠AOE = 20°.
∠DOE = ∠DOB = ∠BOE (як суміжні).
∠DOE = 180° − 20° = 160°.
Відповідь:
160°.
