№ 3.19 Геометрія = № 7.19 Математика
Знайдіть кут між більшою стороною і діагоналлю прямокутника, якщо він:
1. на 90° менший від кута між діагоналями, який лежить проти більшої сторони;
2. на 40° менший від кута між діагоналями, який лежить проти меншої сторони.
Розв'язок:
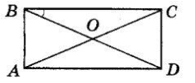
ABCD — прямокутник, AC і BD — діагоналі,
O — точка їх перетину,
BC > AB.
1. Нехай ∠CBO = x, тоді ∠BOC = x + 90°.
∠OBC = ∠OCB як кути при основі рівнобедреного ΔBOC (BO = CO як половини рівних діагоналей). Сума кутів трикутника 180°:
x + x + x + 90 = 180;
3x = 90;
x = 30.
∠OBC = 30°.
2. Нехай ∠CBO = x, тоді ∠AOB = x + 40°.
Тоді ∠BOC = 180° − ∠AOB = 180° − (x + 40°) =
= 180° − x − 40° = 140° − x
(∠AOB і ∠COB — суміжні).
∠BCO = ∠CBO як кути при основі рівнобедреного трикутника BOC (BO = CO як половини рівних діагоналей).
x + x + 140 − x = 180;
x = 180 – 140;
x = 40.
∠CBO = 40°.
Відповідь:
1. 30°;
2. 40°.
