№ 2.36 Геометрія = № 6.36 Математика
Один з кутів паралелограма на 12° більший за другий. Знайдіть кут між висотами паралелограма, проведеними з вершин:
1. гострого кута;
2. тупого кута.
Розв'язок:
Нехай менший кут паралелограма x°, тоді більший кут — (x + 12)°.
Сума гострого і тупого кутів дорівнює 180°:
x + x + 12 = 180;
2x = 168;
x = 84.
Отже, в паралелограмі ABCD:
∠A = ∠C = 84°;
∠B = ∠D = 84° + 12° = 96°.
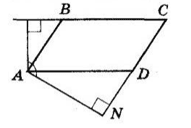
1. AM ⊥ BC, AN ⊥ CD — висоти, проведені з вершини гострого кута A.
Сума кутів чотирикутника AMCN дорівнює 360°:
∠A + ∠M + ∠C + ∠N = 360°;
∠A + 90° + 84° + 90° = 360°;
∠A + 264° = 360°;
∠A = 96°.
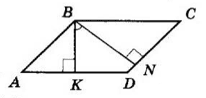
2. BK ⊥ AD, BN ⊥ CD — висоти, проведені з вершини тупого кута B.
Сума кутів чотирикутника KBND дорівнює 360°:
∠KBN + ∠BND + ∠NDK + ∠BKD = 360°;
∠KBN + 90° + 96° + 90° = 360°;
∠KBN + 276° = 360°;
∠KBN = 84°.
Відповідь:
1. 96°.
2. 84°.
