Завдання № 2.37

№ 2.37 Геометрія =  № 6.37 Математика

Доведіть, що три висоти трикутника або їхні продовження перетинаються в одній точці (ортоцентрі трикутника).

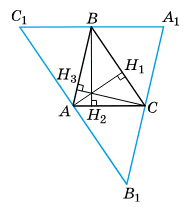
Розв'язок:

1. Нехай AH₁, BH₂, CH₃ — висоти гострокутного трикутника ABC. Проведемо через вершини трикутника прямі, паралельні протилежним сторонам. Одержимо трикутник A₁B₁C₁. Чотирикутник ABA₁C — паралелограм (за побудовою). Тому BA₁ = AC.  
Аналогічно ACBC₁ — паралелограм, C₁B = AC. Отже, C₁B = BA₁, точка B — середина A₁C₁. Оскільки BH₂ ⊥ AC і AC∥A₁C₁, то BH₂ ⊥ A₁C₁. Тому BH₂ належить середньому перпендикуляру до сторони A₁C₁ трикутника A₁B₁C₁. Аналогічно AH₁ і CH₃ належать серединним перпендикулярам до двох інших сторін цього трикутника. Як відомо, серединні перпендикуляри до сторін трикутника перетинаються в одній точці. Отже, AH₁, BH₂ і CH₃ перетинаються в одній точці.  

2. Якщо △ABC — прямокутний, наприклад ∠ C = 90°, то очевидно, що три висоти перетинаються в точці C.  

3. Якщо △ABC — тупокутний, то продовження трьох висот трикутника перетинаються в одній точці. Доведення аналогічне до доведення п. 1.