№ 2.35 Геометрія = № 6.35 Математика
Два кути паралелограма відносяться як 5 : 7. Знайдіть кут між висотами паралелограма, проведеними з вершини:
1. тупого кута;
2. гострого кута.
Розв'язок:
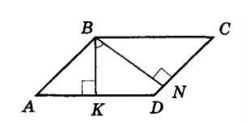
1. ABCD — паралелограм. BK ⊥ AD, BN ⊥ CD — висоти, проведені з вершини тупого кута B. За умовою ∠A : ∠B = 5 : 7.
Нехай x — коефіцієнт пропорційності, тоді
∠A = ∠C = 5x,
∠B = ∠D = 7x.
Сума сусідніх кутів паралелограма дорівнює 180°.
5x + 7x = 180;
12x = 180;
x = 15.
Отже, ∠D = 7 · 15° = 105°.
Сума кутів чотирикутника KBND = 360°:
∠KBN + ∠BND + ∠NDK + ∠BKD = 360°;
∠KBN + 90° + 105° + 90° = 360°;
∠KBN = 360° − 285° = 75°.
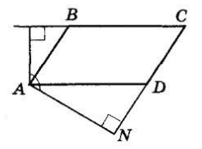
2. ABCD — паралелограм. AM ⊥ BC, AN ⊥ CD — висоти, проведені з вершини гострого кута A.
За умовою ∠A : ∠B = 5 : 7.
Нехай x — коефіцієнт пропорційності, тоді
∠A = ∠C = 5x,
∠B = ∠D = 7x.
Сума сусідніх кутів паралелограма дорівнює 180°:
5x + 7x = 180;
12x = 180;
x = 15.
∠C = 5 · 15° = 75°.
Сума кутів чотирикутника AMCN дорівнює 360°:
∠A + ∠M + ∠C + ∠N = 360°;
∠A + 90° + 75° + 90° = 360°;
∠A + 255° = 360°;
∠A = 105°.
Відповідь:
1. 75°.
2. 105°.
