Завдання № 2.30

№ 2.30 Геометрія =  № 6.30 Математика

У паралелограмі ABCD AB = 6 см, ∠ B = 120°. Висота BK ділить сторону AD на два рівних відрізки. Знайдіть периметр паралелограма.

Розв'язок:

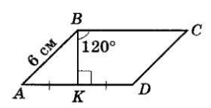
ABCD — паралелограм, тоді ∠A + ∠B = 180°,  
∠A = 180° − ∠B = 180° − 120° = 60°.   
BK ⊥ AD — висота.  
З ΔABK ∠ABK = 90° − ∠A= 90° − 60° = 30°.  
$AK = \frac{1\ }{2}AB = \frac{1\ }{2} · 6 см = 3$ см як катет, що лежить проти кута 30°.  
AD = 2AK = 2 · 3 см = 6 см за умовою.  
P_ABCD = 2(AB + AD) = 2 · (6 + 6) = 24 (см).

Відповідь:

24 см.