№ 2.31 Геометрія = № 6.31 Математика
У паралелограмі ABCD з вершини гострого кута A проведено висоти AL і AK. ∠ LAK = 140°. Знайдіть кут C паралелограма.
Розв'язок:
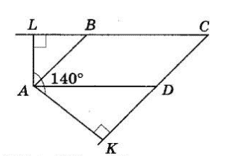
ABCD — паралелограм. AL ⊥ BC, AK ⊥ CD — його висоти.
Оскільки BC∥AD, AB∥CD, то AL ⊥ AD, AK ⊥ AB.
∠LAK = ∠LAD + ∠DAK, ∠DAK = ∠LAK − ∠LAD = 140° − 90° = 50°.
Аналогічно, ∠LAB = ∠LAK − ∠BAK = 140° − 90° = 50°.
∠BAD = ∠LAK – (∠LAB + ∠DAK) = 140° − (50° + 50°) = 40°.
∠C = ∠BAD = 40° як протилежні кути паралелограма.
Відповідь:
40°.
