№ 2.28 Геометрія = № 6.28 Математика
Доведіть, що бісектриси двох сусідніх кутів паралелограма взаємно перпендикулярні.
Розв'язок:
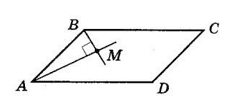
Якщо AM і BM — бісектриси кутів A і B,
то ∠BAM = $\frac{1\ }{2} ∠A, ∠ABM = \frac{1\ }{2} ∠B.$
ABCD — паралелограм,
тому ∠BAM + ∠ABM = $\frac{1\ }{2}(∠A + ∠B) = \frac{1\ }{2} · 180° = 90°.$
З ΔAMB ∠AMB = 180° − (∠BAM + ∠ABM) = 180° − 90° = 90°.
Таким чином, у будь−якому паралелограмі бісектриси його сусідніх кутів перетинаються під прямим кутом.
