№ 2.27 Геометрія = № 6.27 Математика
На сторонах AD і BC паралелограма ABCD позначено точки M і K так, що AM = KC. Доведіть, що BMDK — паралелограм.
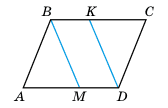
Розв'язок:
1. ABCD — паралелограм, тому AD = BC; AD∥BC.
2. За умовою AM = KC.
3. BK = BC − KC; MD = AD − AM. Тому BK = MD.
4. BK∥MD і BK = MD. Оскільки дві сторони чотирикутника BMDK паралельні й рівні, то за ознакою BMDK є паралелограмом, що й треба було довести.
