№ 2.24 Геометрія = № 6.24 Математика
Побудуйте паралелограм за стороною і діагоналями.
Розв'язок:
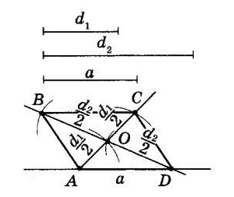
Припустимо, що ABCD — шуканий паралелограм,
O — точка перетину його діагоналей.
Тоді у нього AO = $\frac{d_2}{2}, DO = \frac{d_2}{2}, AD = a. $
У ΔAOD відомі три сторони.
Побудова
1. Будуємо ΔAOD за трьома сторонами:
$AO = \frac{d_1}{2}, DO = \frac{d_2}{2}, AD = a.$
2. На промені AO відкладаємо $OC = \frac{d_1}{2}, $
на промені $DO — OB = \frac{d_2}{2}.$
ABCD — шуканий паралелограм.
