№ 2.23 Геометрія = № 6.23 Математика
У паралелограмі ABCD AB = 4 см, BC = 12 см. Бісектриса кута A перетинає сторону BC у точці P. Знайдіть BP і PC.
Розв'язок:
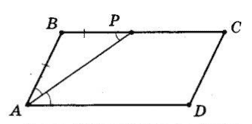
∠BPA = ∠PAD (як внутрішні різносторонні при AD∥BC і січній AP);
∠BAP = ∠PAD (за означенням бісектриси).
Тоді ∠BAP = ∠BPA, тобто ΔABP — рівнобедрений, BP = AB = 4 см.
BC = BP + PC,
PC = BC − BP = 12 см − 4 см = 8 см.
Відповідь:
4 см, 8 см.
