: § 2. Паралелограм, його властивості й ознаки № 2.1 – 2.44

Завдання № 2.22

№ 2.22 Геометрія = № 6.22 Математика

У паралелограмі ABCD бісектриса кута A ділить сторону BC на відрізки BM = 5 см і MC = 7 см. Знайдіть периметр паралелограма.

Розв'язок:

Відповідь до завдання № 2.22 Геометрія

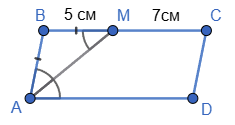
ΔABM — рівнобедрений, оскільки ∠BMA = ∠MAD (як внутрішні різносторонні при AD∥BC і січній AM), а ∠BAM = ∠MAD (за означенням бісектриси).
Отже, AB = BM = 5 см.
BC = BM + MC = 5 см + 7 см = 12 см.
P_ABCD = 2(AB + BC) = 2 · (5 + 12) = 2 · 17 = 34 (см).

Відповідь:

34 см.