№ 1.32 Геометрія = № 5.32 Математика
Доведіть:
1. Доведіть, що △ABC = △CDA, якщо AB = CD і ∠BAC = ∠ACD.
2. Доведіть, що BC = AD і ∠BCA = ∠CAD.
3. Чи паралельні прямі BC і AD?
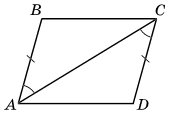
Розв'язок:
1. AB = CD; ∠BAC = ∠ACD (за умовою).
AC — спільна сторона трикутників ABC і CDA.
Тому ΔABC = ΔCDA (за першою ознакою).
2. Оскільки ΔABC = ΔCDA, то BC = AD і ∠BCA = ∠CAD.
3. Оскільки ∠BCA = ∠CAD, і ці кути — внутрішні різносторонні, утворені при перетині прямих BC і AD січною AC, то BC || AD.
