№ 1.25 Геометрія = № 5.25 Математика
Опуклий чотирикутник називають дельтоїдом, якщо він має дві пари рівних сусідніх сторін. Доведіть, що:
1. діагональ BD ділить навпіл і кут B, і кут D;
2. діагоналі дельтоїда взаємно перпендикулярні.
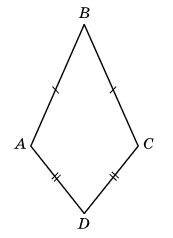
Розв'язок:
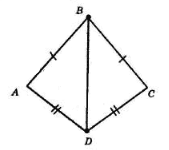
AB = BC; AD = DC (за умовою), BD — спільна сторона трикутників ABD і CBD.
Тому ΔABD = ΔCBD.
1. Оскільки ΔABD = ΔCBD, то ∠ABD = ∠CBD і ∠ADB = ∠CDB.
Отже, діагональ BD ділить навпіл як кут B, так і кут D.
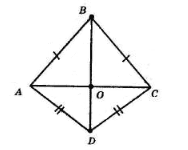
2. BO — бісектриса рівнобедреного трикутника, що проведена до основи. Тому BO є також і висотою.
Отже, BO ⊥ AC, а тому BD ⊥ AC, тобто діагоналі дельтоїда взаємно перпендикулярні.
