Завдання № 10.24

№ 10.24 Геометрія =  № 18.24 Математика

Діагональ рівнобічної трапеції ділить навпіл тупий кут трапеції, а її середню лінію – на відрізки 4 см і 6 см. Знайдіть периметр трапеції.

Розв'язок:

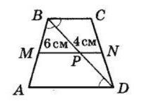
У трапеції ABCD AB = CD, BD — бісектриса кута B, MN — середня лінія, P — точка перетину діагоналі і середньої лінії, MP = 6 см, PN = 4 см.  
MN || BC, MN || AD за означенням середньої лінії. M — середина AB за умовою, тоді P — середина BD за теоремою Фалеса.  
MP = $\frac{1}{2}$ AD як середня лінія ΔABD.  
AD = 2MP = 2 · 6 = 12 (см).  
Аналогічно, в ΔBCD BC = 2PN =
= 2 · 4 = 8 (см).  
∠CBD = ∠BDA як внутрішні різносторонні при BC || AD і січній BD.  
Але ∠CBD = ∠ABD за умовою, тоді ∠ABD = ∠BDA, ΔABD — рівнобедрений, AB = AD = 12 см.  
P_ABCD = AD + 2AB + BC =
= 12 + 2 · 12 + 8 = 44 (см).  

Відповідь:

44 см.