№ 10.23 Геометрія = № 18.23 Математика
У трапеції ABCD (AD || BC) ∠A = 90°, ∠C = 135°, AB = 6 см. Знайдіть середню лінію трапеції, якщо її діагональ перпендикулярна до бічної сторони.
Розв'язок:
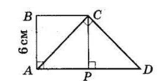
ABCD — трапеція (AD || BC), ∠A = 90°, ∠C = 135°, AB = 6 см, AC ⊥ CD.
∠BCD = ∠BCA + ∠ACD,
∠BCA = ∠BCD − ∠ACD =
= 135° − 90° = 45°.
У ΔABC ∠B = 90°, оскільки ∠A = 90°, a BC || AD, ∠BCA = 45°,
тоді ∠BAC = 45°.
ΔABC — рівнобедрений (кут при основі рівні).
BC = AB = 6 см.
Проведемо CP ⊥ AD.
У ΔACD — ∠D = 180° − ∠BCD =
= 180° − 135° = 45°.
∠ACD = 90°, тоді ∠CAD = 45°. ΔACD — рівнобедрений, AC = CD.
Висота CP є медіаною, AP = PD. Але AP = BC,
тому AD = 2BC = 2 · 6 = 12 (см).
Середня лінія:
$\frac{AD\ +\ BC}{2}=\ \frac{12\ +\ 6}{2}$ = 9 (см).
Відповідь:
9 см.
