№ 10.18 Геометрія = № 18.18 Математика
З вершини B тупого кута рівнобічної трапеції ABCD проведено висоту BK до основи AD. AK = 4 см, BC = 6 см. Знайдіть середню лінію трапеції.
Розв'язок:
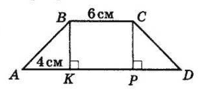
ABCD — трапеція, BK ⊥ AD — висота, AK = 4 см, BC = 6 см.
Проведемо CP ⊥ AD. Чотирикутник KBCP — прямокутник (BC || KP, BK || CP, ∠BKP = 90°).
KP = BC = 6 см, PD = AK = 4 см (з рівності трикутників ABK і DCP за гіпотенузою і гострим кутом).
AD = AK + KP + PD =
= 4 + 6 + 4 = 14 (см).
Середня лінія трапеції дорівнює:
$\frac{BC\ +\ AD}{2}=\ \frac{6\ +\ 14}{2} =\ \frac{20}{2}$ = 10 (см).
Відповідь:
10 см.
