№ 10.16 Геометрія = № 18.16 Математика
У трапеції ABCD M – середина бічної сторони AB, N – середина MB. Через точки M і N проведено прямі, паралельні BC, які перетинають CD у точках K і L відповідно. MK = 12 см, NL = 8 см. Знайдіть основи трапеції.
Розв'язок:
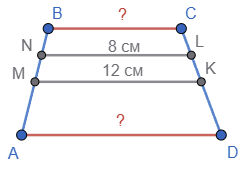
ABCD — трапеція, BC || AD.
MK || BC, значить, MK || AD.
Отже, MBCK — трапеція.
N — середина AB, NL || BC, значить, NL || MK.
За теоремою Фалеса NL — середня лінія трапеції MBCK.
NL =$\frac{BC\ +\ MK}{2};$
8 =$\frac{BC\ +\ 12}{2};$
BC + 12 = 16;
BC = 4 см.
Аналогічно, MK — середня лінія трапеції ABCD.
MK =$\frac{AD\ +\ BC}{2};$
12 =$\frac{AD\ +\ 4}{2};$
AD + 4 = 24;
AD = 20.
Отже, BC = 4 см, AD = 20 см.
Відповідь:
4 см, 20 см.
