№ 10.15 Геометрія = № 18.15 Математика
У трапеції ABCD AD = 30 см, BC = 12 см – основи, а точки E і T – середини AB і AE відповідно. Через E і T проведено прямі, паралельні AD. Знайдіть відрізки цих прямих, що містяться між бічними сторонами трапеції.
Розв'язок:
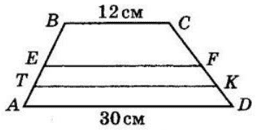
ABCD — трапеція. Точка E — середина AB. EF || AD, оскільки AD || BC, то EF || BC, тоді за теоремою Фалеса F — середина CD.
EF — середня лінія трапеції.
EF =$\frac{AD\ +\ BC}{2} =\ \frac{30\ +\ 12}{2} =$
$= \ \frac{42}{2}$ = 21 (см).
За умовою T — середина AE. TK || AD за умовою. Оскільки AD || EF, то TK || EF. Тоді за теоремою Фалеса K — середина DF, TK — середня лінія трапеції AEKD (EF || AD).
TK =$\frac{EF\ +\ AD}{2} =\ \frac{21\ +\ 30}{2} =$
$= \ \frac{51}{2}$ = 25,5 (см).
Відповідь:
21 см, 25,5 см.
